GAMES202->assignment4 Kulla-Conty BRDF

项目地址：here

PBR

初始状态

float DistributionGGX(vec3 N, vec3 H, float roughness)
{
   // TODO: To calculate GGX NDF here
   return 1.0;  
}
float GeometrySchlickGGX(float NdotV, float roughness)
{
    // TODO: To calculate Smith G1 here   
    return 1.0;
}
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    // TODO: To calculate Smith G here
    return 1.0;
}
vec3 fresnelSchlick(vec3 F0, vec3 V, vec3 H)
{
    // TODO: To calculate Schlick F here
    return vec3(1.0);
}
初始状态

补充公式

float DistributionGGX(vec3 N, vec3 H, float roughness)
{
    float a = roughness*roughness;
    float a2 = a*a;
    float NdotH = max(dot(N, H), 0.0);
    float NdotH2 = NdotH*NdotH;
    float nom   = a2;
    float denom = (NdotH2 * (a2 - 1.0) + 1.0);
    denom = PI * denom * denom;
    return nom / max(denom, 0.0001);
}

float GeometrySchlickGGX(float NdotV, float roughness) {
    float a = roughness;
    float k = (a * a) / 2.0;
    float nom = NdotV;
    float denom = NdotV * (1.0 - k) + k;
    return nom / denom;
}

float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    // TODO: To calculate Smith G here
    float NdotL = max(dot(N,L),0.0);
    float NdotV = max(dot(N,V),0.0);
    return GeometrySchlickGGX(NdotL, roughness)*GeometrySchlickGGX(NdotV, roughness);
}

float Pow5(float x)
{
    return x*x*x*x*x;
}

vec3 fresnelSchlick(vec3 F0, vec3 V, vec3 H)
{
    // TODO: To calculate Schlick F here
    float cosA = max(dot(V,H),0.0);
    float t = Pow5(1.0 - cosA);
    return F0 + (vec3(1.0)-F0) * t;
}
PBR2
image-20210630150640416

roughness=0.35

detail0.35

roughness=0.55

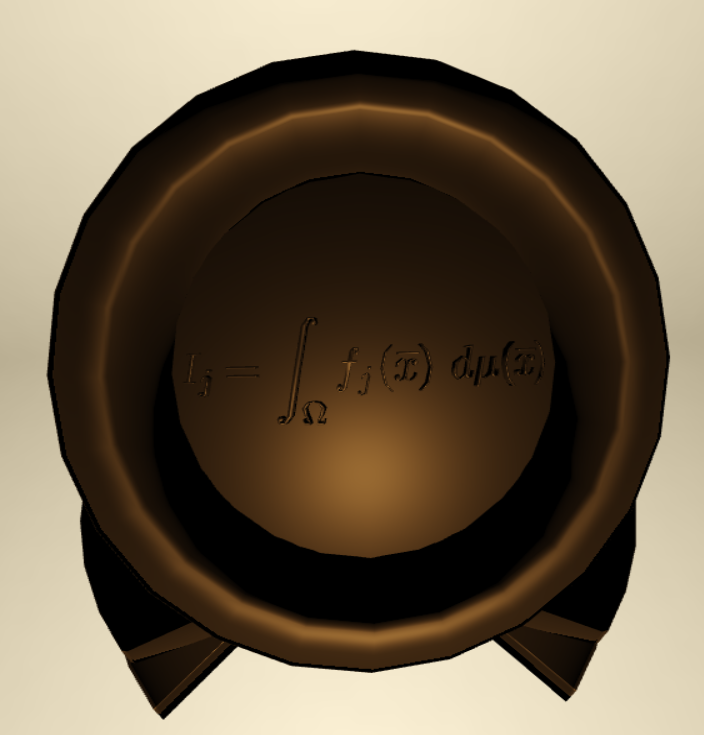
detail0.75

roughness=0.95

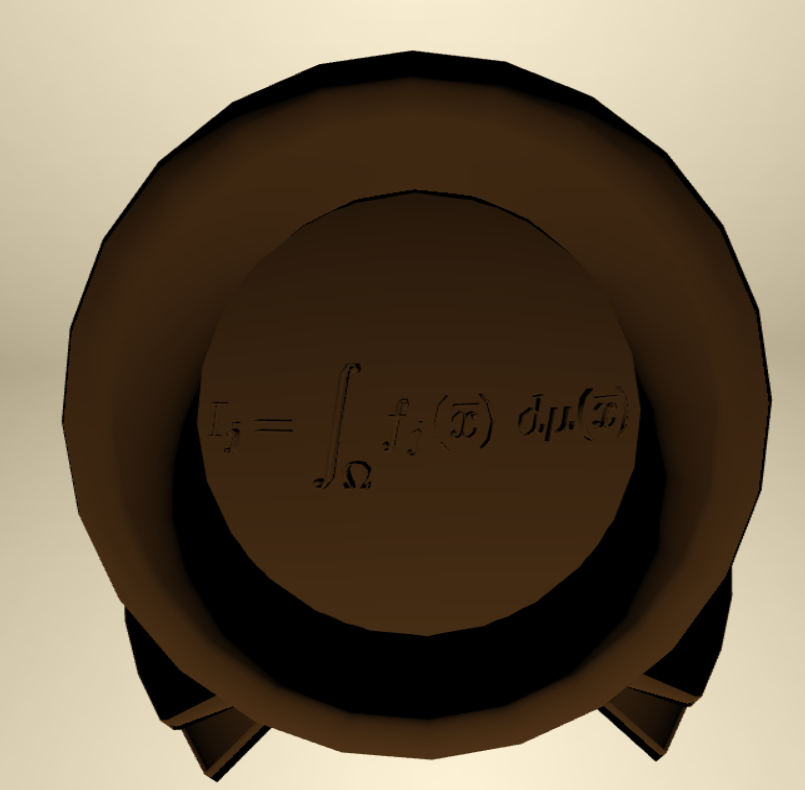
detail0.95

Kulla-Conty

预计算E(μ)

蒙特卡洛方法

Vec3f IntegrateBRDF(Vec3f V, float roughness, float NdotV) {
    float A = 0.0;
    float B = 0.0;
    float C = 0.0;
    const int sample_count = 1024;
    Vec3f N = Vec3f(0.0, 0.0, 1.0);
	float R0 = 1.0f;
    samplePoints sampleList = squareToCosineHemisphere(sample_count);
    for (int i = 0; i < sample_count; i++) {
      // TODO: To calculate (fr * ni) / p_o here
		Vec3f L = normalize(sampleList.directions[i]);
		Vec3f H = normalize(V + L);
		float cosA = std::max(0.0f,dot(V,H));
		float NdotL = std::max(dot(N, L), 0.0f);
		float F = R0 + (1.0f-R0)*pow(1- cosA,5.0f);
		float G = GeometrySmith(roughness, NdotV, NdotL);
		float D = DistributionGGX(N,H,roughness);
		float numerator = D * G * F;
		float denominator = 4.0f * NdotV * NdotL;
		float Fmicro = numerator / std::max(denominator, 1e-7f);
		float pdf = sampleList.PDFs[i];
		A += Fmicro * NdotL / pdf;
    }
	B = C = A;
    return {A / sample_count, B / sample_count, C / sample_count};
}
GGX_E_MC_LUT

重要性采样

Vec3f ImportanceSampleGGX(Vec2f Xi, Vec3f N, float roughness) {
    float a = roughness * roughness;

    //TODO: in spherical space - Bonus 1
	float Phi = 2 * PI * Xi.x;
    //TODO: from spherical space to cartesian space - Bonus 1
	float CosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
	float SinTheta = sqrt(1.0 - CosTheta * CosTheta);

	Vec3f H;
	H.x = SinTheta * cos(Phi);
	H.y = SinTheta * sin(Phi);
	H.z = CosTheta;

    //TODO: tangent coordinates - Bonus 1
	Vec3f UpVector = abs(N.z) < 0.999 ? Vec3f(0.0f, 0.0f, 1.0f) : Vec3f(1.0f, 0.0f, 0.0f);
	Vec3f TangentX = normalize(cross(UpVector, N));
	Vec3f TangentY = cross(N, TangentX);
    //TODO: transform H to tangent space - Bonus 1
	Vec3f result = TangentX * H.x + TangentY * H.y + N * H.z;
	return normalize(result);
}

float GeometrySchlickGGX(float NdotV, float roughness) {
    // TODO: To calculate Schlick G1 here - Bonus 1
	float a = roughness;
	float k = (a * a) / 2.0f;

	float nom = NdotV;
	float denom = NdotV * (1.0f - k) + k;

	return nom / denom;
}

Vec3f IntegrateBRDF(Vec3f V, float roughness) {
	float A = 0.0;
	float B = 0.0;
	float C = 0.0;
	float R0 = 1.0f;

    const int sample_count = 1024;
    Vec3f N = Vec3f(0.0, 0.0, 1.0);
    for (int i = 0; i < sample_count; i++) {
        Vec2f Xi = Hammersley(i, sample_count);
        Vec3f H = ImportanceSampleGGX(Xi, N, roughness);
        Vec3f L = normalize(H * 2.0f * dot(V, H) - V);

        float NoL = std::max(L.z, 0.0f);
        float NoH = std::max(H.z, 0.0f);
        float VoH = std::max(dot(V, H), 0.0f);
        float NoV = std::max(dot(N, V), 0.0f);
        
		float cosA = VoH;
		float F = R0 + (1.0f - R0)*pow(1 - cosA, 5.0f);
        // TODO: To calculate (fr * ni) / p_o here - Bonus 1
		A += F * VoH * GeometrySmith(roughness,NoV, NoL) / (NoV*NoH);      
    }
	B = C = A;
	return { A / sample_count, B / sample_count, C / sample_count };
}
GGX_E_LUT

1-Eμ检验

Vec3f IntegrateBRDF(Vec3f V, float roughness) {
	float A = 0.0;
	float B = 0.0;
	float C = 0.0;
	float R0 = 1.0f;

    const int sample_count = 1024;
    Vec3f N = Vec3f(0.0, 0.0, 1.0);
    for (int i = 0; i < sample_count; i++) {
	    //... some code
        // TODO: To calculate (fr * ni) / p_o here - Bonus 1
		A += F * VoH * GeometrySmith(roughness,NoV, NoL) / (NoV*NoH);        
    }
	B = C = A = 1 - A;
	return { A / sample_count, B / sample_count, C / sample_count };
}
1-Eu

预计算Eavg

蒙特卡洛方法

Vec3f IntegrateEmu(Vec3f V, float roughness, float NdotV, Vec3f Ei) {
    Vec3f Eavg = Vec3f(0.0f);
    const int sample_count = 1024;
    Vec3f N = Vec3f(0.0, 0.0, 1.0);

    samplePoints sampleList = squareToCosineHemisphere(sample_count);
    for (int i = 0; i < sample_count; i++) {
        Vec3f L = sampleList.directions[i];
        Vec3f H = normalize(V + L);

        float NoL = std::max(L.z, 0.0f);
        float NoH = std::max(H.z, 0.0f);
        float VoH = std::max(dot(V, H), 0.0f);
        float NoV = std::max(dot(N, V), 0.0f);

        // TODO: To calculate Eavg here
		Eavg += Ei * NoV*2.0f;
    }

    return Eavg / sample_count;
}
GGX_Eavg_LUT

重要性采样

GGX_Eavg_LUT

实时计算

vec3 MultiScatterBRDF(float NdotL, float NdotV)
{
  vec3 albedo = pow(texture2D(uAlbedoMap, vTextureCoord).rgb, vec3(2.2));

  vec3 E_o = texture2D(uBRDFLut, vec2(NdotL, uRoughness)).xyz;
  vec3 E_i = texture2D(uBRDFLut, vec2(NdotV, uRoughness)).xyz;

  vec3 E_avg = texture2D(uEavgLut, vec2(0, uRoughness)).xyz;
  // copper
  vec3 edgetint = vec3(0.827, 0.792, 0.678);
  vec3 F_avg = AverageFresnel(albedo, edgetint);
  
  // TODO: To calculate fms and missing energy here
  vec3 fms = (vec3(1.0)-E_o)*(vec3(1.0)-E_i)/(PI*(vec3(1.0)-E_avg));
  vec3 F_add = F_avg*E_avg/(vec3(1.0)-F_avg*(vec3(1.0)-E_avg));

  return F_add*fms;  
}
kulla-conty2
image-20210630234150696